GRE® Probability Practice Question 7

This GRE quant practice question is a probability problem solving question. A classic question testing your understanding of selecting two objects from a set in the context of a chess board. Level of difficulty: Hard

Question 7: What is the probability that two squares(smallest dimension) selected randomly from a chess board will have only one common corner?

1. \\frac{7}{288})
2. \\frac{7}{144})
3. \\frac{7}{126})
4. \\frac{7}{72})
5. \\frac{2}{63})

---

---

Video Explanation

---

---

Explanatory Answer | GRE Probability Question 7

Step 1: Compute the number of ways to selecting two 1 x 1 squares at random.

There are 64 (1 x 1) squares in a chess board.
The number of ways of selecting two out of 64 squares is 64 choose 2 or 64C₂

---

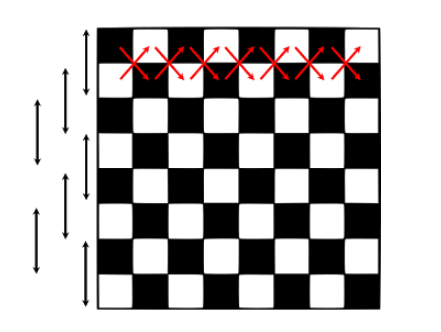
Step 2: Count number of 1 x 1 squares that have only one common corner

Let us consider the first and second row of the chess board in the diagram given above.
The red arrows mark the pairs of squares that share only one corner.
In the first and second row, there are 14 ways of selecting two (1 x 1) squares that have only one common corner.
Rows 2 and 3 will similarly have 14 squares that have only one common corner.
We can pick 7 such pairs of rows in a chess board viz., (1, 2), (2, 3), (3, 4), (4, 5), (5, 6), (6, 7), and (7, 8).
Therefore, the number of ways of selecting two (1 x 1) squares in a chess board that have only one common corner = 14 × 7 = 98.

Required probability = \\frac{\text{Number of ways of selecting 2 squares that have only one common corner}}{\text{Number of ways of selecting 2 squares from a chessboard}})
= \\frac{98}{{^{64}}{C}_{2}}) = \\frac{98 × 2}{64 × 63}) = \\frac{7}{144})

---

Try these variants

1) What is the probability that a pair of 1 x 1 square selected at random in a chess board has only one common side?
2) What is the probability of selecting a white square and a black square in a chess board such that the two squares do not lie on the same row or same column?