GRE® Quant Practice | Geometry

This GRE quant practice question is a problem solving question in geometry - circles. Area of a sector of a circle, area of minor segment, and area of major segment of a circle.

Question 3 : Chord AC at a distance of 7 cm from the center of a circle subtends an angle of 120 degrees at the center. What is the area of major segment?

1. 410 \\frac{1}{3}) + 7√3 cm²
2. 410 \\frac{1}{3}) + 49√3 cm²
3. 1232 + 49√3 cm²
4. 1232 + 7√3 cm²
5. 410 \\frac{2}{3}) + 49√3 cm²

---

---

Video Explanation

---

---

Explanatory Answer | GRE Geometry Practice Question 3

Step 1 of solving this question: Compute the radius of the circle

In the figure AC is the chord and the angle that it subtends at the center of the circle is ∠AOC.
OA and OC are radii to the circle.
Draw OD perpendicular to AC.
ΔODC and ΔODA are congruent right triangles. (RHS test)
Hence, AD equals DC

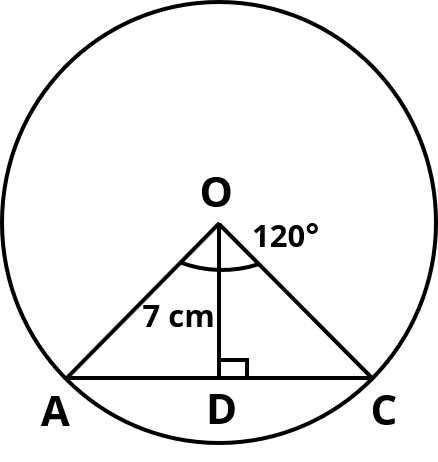
And ∠AOD = ∠COD = 60°
Because ∠COD = 60° and ∠CDO = 90°, ∠OCD = 30°
So, Δ ODC is a 30 - 60 - 90 right triangle.

The sides opposite 30° – 60° – 90° will be in the ratio 1 : √3 : 2
The side opposite 30° is OD = 7 cm
So, the side opposite 90° ⇒ OC = 2 × 7 = 14 cm
The radius OC = 14 cm.
Let us also compute CD = √3 × 7 = 7√3 cm

Step 2 of solving this question: Compute the area of the sector AOC

Area of sector = \\frac{θ}{360}) × π r², where θ is the angle subtended by the chord at the centre of the circle
Chord AC subtends an angle of 120° at the center of the circle.
So, area of sector AOC = \\frac{120}{360}) × \\frac{22}{7}) × 14 × 14
Area of sector AOC = \\frac{616}{3}) cm²

Step 3 of solving this question: Compute the area of triangle AOC

Area of a triangle = \\frac{1}{2}) × base × height
Base of the triangle, AC = 2 × CD
In step 1, we computed CD = 7√3. So, AC = 14√3
Area of triangle AOC = \\frac{1}{2}) × 14√3 × 7 = 49√3

Step 4 of solving this question: Compute the area of minor segment

Area of minor segment = Area of sector ABC – Area of triangle AOC
Area of minor segment = \\frac{616}{3}) - 49√3 cm²

Step 5 of solving this question: Compute the area of major segment

Area of major segment = Area of circle – Area of minor segment
Area of a circle = π r² = \\frac{22}{7}) × 14 × 14 = 616 cm²
Area of minor segment = \\frac{616}{3}) - 49√𝟑 cm²
Area of major segment = 616 - (\\frac{616}{3}) - 49√3 cm²) = \\frac{1232}{3}) + 49√𝟑
Area of major segment = 410\\frac{2}{3}) + 49√3

Choice E is the correct answer