GRE® Coordinate Geometry Practice #1

This GRE quant practice question is a coordinate geometry problem solving question. Concepts tested: Properties of right triangles.
1. Where does the orthocenter of a right triangle lie?
2. Where does the circumcenter of a right triangle lie?
3. Computing the length of the line segment joining two points.

Question 1 : A straight line 4x + 3y = 24 forms a triangle with the coordinate axes. What is the distance between the orthocentre of the triangle and the centre of the circle that circumscribes the triangle?

1. 10 units
2. 5 units
3. 13 units
4. 12 units
5. 9 units

---

---

Video Explanation

Play Video: GRE Coordinate Geometry Length of Median to hypotenuse Video Solution

---

---

Explanatory Answer

Step 1 : Compute the coordinates of the 3 vertices of the triangle

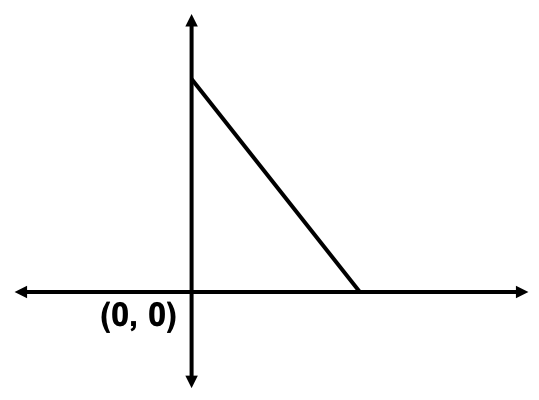
The diagram shows the triangle formed by line 4x + 3y = 24 and the coordinate axes.
As the two coordinate axes are perpendicular to each other, the triangle formed is a right triangle, right angled at the origin.
One of the vertices is the origin. The x-intercept and the y-intercept of the line 4x + 3y = 24 will be the other two vertices of the triangle.
Compute x-intercept: Substitute y = 0 in 4x + 3y = 24. x = 6
Compute y-intercept: Substitute x = 0 in 4x + 3y = 24. y = 8

---

Step 2 : Determine the coordinates of the orthocentre

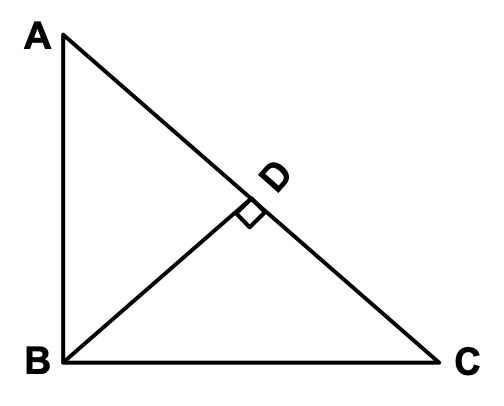
Right triangle ABC shown in the diagram, is right angled at vertex B.
The orthocentre of a triangle is the point at which the 3 altitudes of the triangle meet concurrently.
Because the triangle is right angled at B, altitude to side BC is side AB.
Similarly, altitude to side AB is side BC.
Altitude to side AC, BD will be drawn from vertex B.
So, all 3 altitudes AB, BC and BD meet at B.
So, the coordinates of the orthocentre are (0, 0)

---

Step 3 : Determine the coordinates of the circumcentre

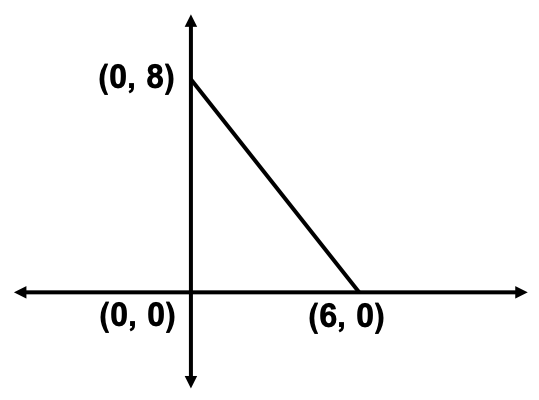
The midpoint of the hypotenuse of a right triangle is its circumcentre.
The coordinates of the midpoint of the line segment joining the points (6, 0) and (0, 8) are the coordinates of the circumcentre of the triangle.
The coordinates of the midpoint of a line segment joining points (x₁, y₁) and (x₁, y₁) are (\\frac{x_1 + x_2}{2}) , \\frac{y_1 + y_2 }{2}))
The coordinates of the midpoint of a line segment joining points (6, 0) and (0, 8) are \\frac{0 + 6}{2}), \\frac{0 + 8}{2}) = (3, 4)

---

Step 4 : Compute the length of the line segment

The length of the line segment AB joining two points A(x₁, y₁) and B(x₂, y₂) is \\sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2})
Hence, the distance between the orthocentre and the circumcentre of the triangle is the length of the line segment joining points (0, 0) and (3, 4).
The distance = \\sqrt{(3 - 0)^2 + (4 - 0)^2}) = \\sqrt{9 + 16}) = \\sqrt{25}) = 5 units

Choice A is the correct answer

Key Takeaways

The circumcentre of a right triangle is at the midpoint of the hypotenuse.
The distance between the circumcentre to any of the vertices measures the circumradius.
So, the circumradius of a right triangle is half the hypotenuse.