GMAT Math Questions | Coordinate Geometry Q3

The question given below is a GMAT data sufficiency practice question in coordinate geometry. The concept tested is determining the quadrants through which a line passes and the nature of the point of intersection of two perpendicular lines. A GMAT Hard Math Question - A GMAT 700 level DS question.

GMAT Data Sufficiency | Directions | Click Here ▼

This data sufficiency problem consists of a question and two statements, labeled (1) and (2), in which certain data are given. You have to decide whether the data given in the statements are sufficient for answering the question. Using the data given in the statements, plus your knowledge of mathematics and everyday facts (such as the number of days in a leap year or the meaning of the word counterclockwise), you must indicate whether -

1. Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
2. Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
3. BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question asked.
4. EACH statement ALONE is sufficient to answer the question asked.
5. Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.

Numbers

All numbers used are real numbers.

Figures

A figure accompanying a data sufficiency question will conform to the information given in the question but will not necessarily conform to the additional information given in statements (1) and (2)

Lines shown as straight can be assumed to be straight and lines that appear jagged can also be assumed to be straight

You may assume that the positions of points, angles, regions, etc. exist in the order shown and that angle measures are greater than zero.

All figures lie in a plane unless otherwise indicated.

Note

In data sufficiency problems that ask for the value of a quantity, the data given in the statement are sufficient only when it is possible to determine exactly one numerical value for the quantity.

Question 3: Line L is perpendicular to line K whose equation is 3y = 4x + 12; Lines L and K intersect at (p, q).
Is p + q > 0?

Statement 1: x intercept of Line L is less than that of Line K
Statement 2: y intercept of Line L is less than that of Line K

---

---

Video Explanation

---

---

Explanatory Answer | GMAT Coordinate Geometry DS

Step 1: Decode the Question Stem

Q1. What kind of an answer will the question fetch?
An "Is" question will fetch "Yes" or a "No" as an answer.
The data is sufficienct if we get a definite yes or definite no as the answer from the data available in the statements.

Q2. What information is available from the question stem?

1. Equation of line K is 3y = 4x + 12. It is a positive sloping line intercepting the x axis at (-3, 0) and the y axis at (0, 4).
2. Line L is perpendicular to line K. The coordinates of the point of intersection of lines L and K are (p, q).
3. If (p, q) is in the first quadrant, then p + q > 0. If (p, q) is in the third quadrant, then p + q < 0. If the point is in the II or the IV quadrant we will need specific inputs about the point of intersection to determine whether p + q is positive.

---

Step 2: Evaluate Statement 1 ALONE

Statement 1: x intercept of Line L is less that that of Line K.

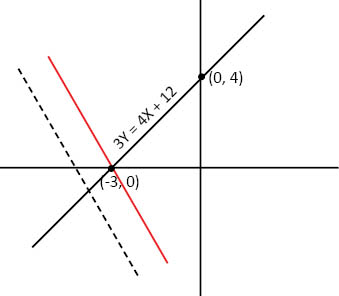
The red line represents the scenario where lines L and K, both have the same x - intercept i.e., (-3, 0)
However, as per statement 1, the x intercept of line L is less than that of line K.
So, the dotted line represents line L. If the x intercept of line L is less than that of line K, the point of intersection of the two lines will be further to the left of (-3, 0).
It is quite evident from the diagram that the two lines will therefore, intersect in the III quadrant.
Any point in the III quadrant will have negative x and y values.
Therefore, p + q < 0.

We are able to answer the question with a DEFINITE NO using Statement 1.
Hence, statement 1 alone is sufficient.
Eliminate answer option B, C, and E.
Choices narrow down to A or D.

---

Step 3: Evaluate Statement 2 ALONE

Statement 2: y intercept of Line L is less than that of Line K.

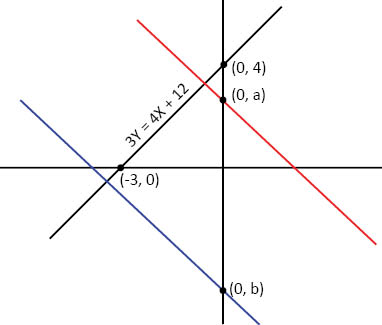
In the above diagram two variants for line L are presented.
Option 1: In the variant where line L is in red, the y intercept of L is less than that of line K at (0, a). It can be seen that the point of intersection of line L (red) and line K (black line) is in the second quadrant. In the 2^nd quadrant x coordinate is negative and y coordinate is positive.
Therefore, p + q could be positive or negative or 0.

Option 2: In the variant where line L is represented in blue, the y intercept of L is less than that of line K at (0, b). It can be seen that the point of intersection of line L (blue) and line K (black) is in the 3^rd quadrant. Here p + q < 0.
As we are not sure from statement 2 which of the options line L could be, we cannot get a definite answer to the question.

We are unable to answer the question with a DEFNITE YES/NO using Statement 2.
Hence, statement 2 alone is not sufficient.
Eliminate answer option D.

Statement 1 ALONE is sufficient, while statement 2 is not.

Choice A is the correct answer.